Introduction
The concept of focal length is a fundamental pillar in optics, helping elucidate the behavior of light rays and their interactions with optical elements. Focal length is applied in the crafting of lenses in telescopes, cameras, and corrective eyewear for individuals with refractive errors. Focal length governs the convergence or divergence of light rays, dictating the precise point where they either converge to form an image or diverge from an origin.[1][2]
From the intricate mechanisms of the human eye to the design of advanced imaging systems, understanding focal length holds paramount importance. The following sections will explore the nuances of focal length, its mathematical underpinnings, its manifestations in optical aberrations, and its crucial implications for medical applications.[1]
Function
Register For Free And Read The Full Article
Search engine and full access to all medical articles
10 free questions in your specialty
Free CME/CE Activities
Free daily question in your email
Save favorite articles to your dashboard
Emails offering discounts
Learn more about a Subscription to StatPearls Point-of-Care
Function
Focal length is the distance between the lens and the focal point, where the light rays converge or diverge. It is a critical parameter that determines the image quality and magnification of optical systems, including the human eye.[3]
The Vergence of Light
The concept of vergence is crucial to understanding why lenses refract light and how to determine the focal length. Vergence is the angle at which light rays converge or diverge as they pass through a lens. Converging light has a positive vergence, and diverging light has a negative vergence. Vergence is determined by the curvature of the lens surfaces and the refractive index of the material.[4]
Converging or convex lenses are thicker at their center and thinner at their edges. Convex lenses bring parallel light rays together to converge at a specific point on the other side of the lens and create an image in front of the lens. The point where the light rays converge is the focal point; the distance from the lens to the focal point is the focal length of the lens.[5] (See Image. Schematic: Convex Lens.) Light rays passing through a convex lens bend or refract toward the center of the lens. The curvature of the lens surface determines the degree of bending or refraction. As a result, these rays converge to a focal point located at a specific distance from the lens. The focal length of the lens determines the degree of convergence. The closer an object is to the lens, the farther away the image is projected. (See Image. Photograph: Convex Lens.)
Diverging or concave lenses have a thinner center and thicker edges. These lenses cause parallel light rays to spread out or diverge as they pass through the lens. Diverging lenses have a virtual focal point from which the divergent rays appear to originate when projected backward, creating an image behind the lens.[4] (See Image. Schematic: Concave Lens.) Light rays that pass through a diverging lens spread out, and when projected backward, they appear to converge at a virtual focal point behind the lens. The focal length of a diverging lens is deemed negative due to this virtual focal point.[4] (See Image. Photograph: Concave Lens.)
Lensometry
The focal length of a lens can be measured via various methods as dictated by the precision required and the lens type. The most commonly used method of measuring focal length in clinical practice is lensometry, a procedure performed using a lensmeter, focimeter, or vertometer. Lensmeters project a parallel beam of light onto a lens and measure the position of the focal point. The lensometer works by projecting a parallel beam of light onto the lens and then measuring the position of the focal point. Lensometry may be used to measure the focal length of spectacle lenses, rigid gas permeable or polymethyl methacrylate (PMMA) contact lenses, and intraocular lenses.[6]
Focal Length Calculations
Several equations are used in optics, optometry, and ophthalmology to calculate the focal length and power of lenses needed to correct refractive errors, such as myopia, hyperopia, and astigmatism.[7]
Thin Lens Equation
One method of determining the focal length of a thin lens in air is the thin lens equation, which relates the focal length of a lens to the distance between the lens and the object. Focal length is always represented in meters. Lens powers are represented in diopters. The thin lens equation is given by,
- 1/f = 1/o + 1/i
in which f = focal length, o = the object distance, and i = the image distance.
The thin lens equation is a simplified version of the formula for the focal length of a refracting surface, specifically designed for thin lenses. The thin lens equation assumes that the thickness of the lens is negligible compared to the radii of curvature of the lens surfaces.
Compound Lens Equation
The focal distances are additive for adjacent lenses, given by,
- 1/f = 1/f1 + 1/f2
in which f = the combined focal length of the adjacent lenses, f1 = the focal length of the first lens, and f2 = the focal length of the second lens.
When two thin lenses are placed a certain distance apart, the focal distance of this "compound lens system" can be calculated by,
- 1/f = 1/f1 + 1/f2 - d/(f1 · f2)
in which f = the focal length of the combined lenses, f1 = the focal length of the first lens, f2 = the focal length of the second lens, and d = the distance between the two lenses.
Lens Maker Equation
When the radii of curvature of the front and back surface and the refractive index of the material of a lens are known, the formula for calculating the focal length of the lens is derived from the lens maker formula given by,
- 1/f = (n - 1) · [(1/R1) - (1/R2)]
in which f = focal length of the refracting surface, n = index of refraction of the lens, R1 = radius of curvature of the refracting surface facing the initial medium, and R2 = radius of curvature of the refracting surface facing the final medium. R values will be positive for concave lenses and negative for convex lenses.
When a lens is placed in a medium other than air, which has a refractive index of approximately 1.0, the lens maker formula is modified slightly. This modification is given by,
- 1/f = [(nl - nm)/nm] · [(1/R1) - (1/R2)]
in which nl = index of refraction of the lens and nm = index of refraction of the medium.
Thick Lens Equation
The lens maker formula can be further modified to accommodate a "thick" lens to account for the distance light rays must travel through the lens itself. This modification gives a more accurate calculation of the focal length.[8] The thick lens equation for a lens in air is given by,
- 1/f = (n - 1) · (1/R1 - 1/R2 + {[(n-1)d]/(n·R1·R2)})
in which f = focal length of the refracting surface, n = index of refraction of the lens, d = distance between the two refracting surfaces R1 and R2 (the thickness of the lens), R1 = radius of curvature of the refracting surface facing the initial medium, and R2 = radius of curvature of the refracting surface facing the final medium. R values will be positive for concave lenses and negative for convex lenses.
If the thick lens is in a medium other than air, the value of (n -1) can be replaced with [(nl - nm)/nm], in which nl = index of refraction of the lens and nm = index of refraction of the medium.
Issues of Concern
Focal length plays a significant role in optical aberrations within the eye. Optical aberrations are deviations from ideal optical performance that can impact the quality and clarity of vision. Several factors, including the shape and size of the eye, the curvature of the cornea and lens, and the presence of refractive errors, can contribute to optical aberrations.[9]
Spherical Aberrations
Spherical aberrations occur when light rays passing through the periphery of a refracting surface focus on a different point than rays passing through the center of the same refracting surface. A lens with a shorter focal length has a steeper curvature, resulting in greater refraction of light rays passing through its periphery and a greater deviation in focal points. Therefore, a lens with a shorter focal length exhibits more spherical aberration than one with a longer focal length. Aspheric lenses can be used to correct spherical aberrations. Aspheric lenses are designed with a nonuniform surface curvature that counters the unequal bending of light rays at the periphery of a spherical lens. This design helps achieve a single focal point, reducing spherical aberration and improving image clarity.[10] (See Image. Lens with Spherical Aberration.)
Astigmatism
Astigmatism is a refractive error in which refraction varies in the different meridians of the eye. The light rays passing through the eye cannot converge at a single focal point but form focal lines. If the cornea or lens has an oval surface or unequal refractive power, there will be different focal distances in different meridians, light rays will be focused at multiple points, and vision will be blurred or distorted. Depending on which focal distance coincides with the position of the retina, images focused by the astigmatic eye may appear smeared or have a shadow in a particular orientation.[11]
Myopia
Myopia, or nearsightedness, occurs when the eye axial length is longer than normal, or the cornea is overly curved, causing light rays to focus in front of the retina rather than directly on it. The focal length of the refracting cornea and crystalline lens in the myopic eye is shorter than the ideal focal length; distant objects appear blurred, while near objects are seen more clearly.[12][9] Myopia can be corrected using concave lenses with a minus power focal length, which increases the focal length of the resulting compound lens comprising the refractive correction, cornea, and crystalline lens. The compound lens system shifts the focus of light onto the retina and improves distance vision.
Hyperopia
Hyperopia, or farsightedness, occurs when the eye axial length is shorter than normal, or the cornea is less curved, causing light rays to focus behind the retina instead of directly on it. The focal length of the hyperopic eye is longer than the ideal focal length, making near objects appear blurred while distant objects may be seen more clearly.[13] Hyperopia can be corrected using convex lenses with a plus power focal length, which decreases the focal length of the compound lens system comprising the refractive correction, cornea, and crystalline lens. The compound lens system shifts the focus of light onto the retina and improves distance and near vision.[13]
Presbyopia
Presbyopia is an age-related condition that typically begins around 40 years of age when the natural crystalline lens loses flexibility. Flexing of the crystalline lens increases the curvature of its surface, decreasing the focal length of the lens and allowing the convergence of divergent light. Since near objects form more divergent light than distant objects, the impaired ability to change shape and accommodate affects near vision. As the lens gradually loses its ability to accommodate, the effective focal length of the eye increases, leading to increasing difficulty in near-vision tasks.[14][15] Presbyopia is typically managed using single-vision reading, bifocal, trifocal, or progressive addition lenses, which add plus focal power to the compound lens system to improve near vision.[14]
Clinical Significance
Focal length calculations are important when managing common eye conditions such as cataracts and evaluating patients for refractive surgical therapy.
Intraocular Lens Power Calculations
The intraocular lens (IOL) power determines its focal length. The IOL power is calculated using the length of the eye determined by ultrasound and the focal length of the cornea determined by keratometry. Inserting an IOL will create a compound lens system comprising the IOL and the cornea; the exact position of the IOL within the eye is another critical factor. These values, along with necessary adjustment factors, are used by cataract surgeons to provide accurate refractive outcomes following cataract surgery.[16]
Light Adjustable Intraocular Lenses
Light adjustable IOLs allow for a change in the focal length of the IOL after it has been implanted. This breakthrough technology uses light to polymerize macromolecules in the IOL and carefully adjust its spherical and astigmatic power. Light is used to manipulate the curvature of the anterior surface of the IOL and achieve ideal focal lengths.[17]
Multifocal and Accommodating Lenses
Multifocal and accommodating IOLs are designed to improve vision at various distances, reducing patient dependence on corrective eyewear. Selecting the appropriate focal length for these IOLs is crucial to optimize visual acuity and minimize side effects, such as halos or reduced contrast sensitivity. Careful patient selection and a thorough preoperative assessment ensure successful outcomes with these specialized IOLs.[18][19]
Multifocal IOLs are designed with multiple optical zones, similar to multifocal eyeglass lenses. These zones allow the eye to focus on objects at varying distances, such as near, intermediate, and far. Multifocal IOLs can reduce dependence on eyeglasses for particular visual tasks such as reading, using digital devices, and engaging in distance activities.[20]
Accommodating IOLs mimic the natural ability of the eye to change shape or accommodate and adjust its focal point to view objects at different distances. The flexible optics of accommodating IOLs permit changes in curvature and provide a range of clear vision from far to near. Patients with accommodating IOLs can experience a more natural and continuous transition as they shift their gaze between objects at different distances, similar to the function of a healthy, natural lens.[21]
Refractive Surgery
Refractive surgery aims to correct refractive errors, such as myopia, hyperopia, and astigmatism, by modifying the curvature of the cornea or replacing the lens. Refractive surgeries like laser-assisted in-situ keratomileusis (LASIK) and photorefractive keratectomy (PRK) aim to optimize the ability of the cornea to focus light onto the retina.
During LASIK, a flap is created on the cornea, and a laser is used to reshape the underlying corneal tissue. The selective removal of corneal tissue modifies the corneal curvature, altering its refractive power and adjusting the focal length. During PRK, the corneal outer layer is removed before reshaping the cornea using an excimer laser. Both procedures aim to achieve the focal length necessary to correct the underlying refractive error.[22]
The extent of corneal tissue removal during refractive surgery directly affects the resulting focal length. In myopia correction, corneal tissue is removed centrally to flatten the cornea, increase its focal length, and allow light rays to converge on the retina. In hyperopia correction, corneal tissue is removed peripherally to steepen the cornea, reduce its focal length, and focus light rays on the retina. Astigmatism correction alters the corneal shape to eliminate irregularities and adjust the focal length in different meridians.[23] Precisely calculating the desired focal length is essential to achieving the intended refractive correction. Failure to accurately determine the appropriate focal length can result in undercorrection, overcorrection, or optical aberrations, leading to suboptimal visual outcomes.[24][25]
Other Issues
Focal length is a critical aspect of designing the optical systems used in many medical fields.
Endoscopy
Endoscopy is a widely used medical procedure that permits the visual examination of many internal anatomical structures. An endoscope is a rigid or flexible tube with a camera attached at one end. The focal length of the endoscopic camera lens determines the distance over which objects in the field of view remain in sharp focus. A shorter focal length results in a shallower depth of field; objects beyond this depth appear blurred. A longer focal length provides a greater depth of field, and a larger range of distances can be captured in sharp focus. The focal length of the endoscopic lens is adjustable; the chosen focal length is dictated by the procedure being performed and the anatomy being examined. Some endoscopes have a "near-focus" mode and a "traditional" mode to vary the size and clarity of the visual field. For example, during gastrointestinal endoscopy, a shorter focal length may be preferred to examine mucosal details closely. In contrast, during bronchoscopy, a longer focal length may be more suitable for visualizing deeper structures of the pulmonary tree.[26][27]
Microscopy
Focal length is a critical parameter in high-resolution imaging of microscopic specimens. Microscopes utilize objective lenses with different focal lengths to focus light and magnify the subject. Researchers and clinicians adjust this magnification to achieve the proper depth of focus for various applications, including histopathology and cytology.[28]
Radiology
The distance between an x-ray source and an image receptor affects the focal length and determines the magnification and resolution of the resulting image. When the x-ray source is closer to the image receptor, the focal length is shorter, resulting in increased image magnification. Conversely, a longer focal length leads to reduced magnification. The size of the focal spot, the area on the x-ray tube from where x-rays are emitted, is another important consideration related to focal length in radiography. A smaller focal spot size allows for improved spatial resolution and finer detail in the radiographic image. However, a smaller focal spot size typically corresponds to a longer focal length, which can result in decreased magnification. Choosing the appropriate focal length and focal spot size allows radiologists to achieve the desired level of image magnification and resolution for accurate diagnosis.[29][30]
Minimally Invasive Surgical Techniques
Focal length is relevant in minimally invasive surgical procedures, such as traditional or robotic-assisted laparoscopy. Laparoscopic camera systems use lenses with adjustable focal lengths to visualize the surgical field. Surgeons can manipulate the focal length to enhance depth perception and magnification, aiding in the precise manipulation of instruments and improving visualization during procedures.[31]
Enhancing Healthcare Team Outcomes
The interprofessional collaboration between ophthalmologists, optometrists, ophthalmic technicians, opticians, nurses, pharmacists, and other health professionals ensures that patients receive optimal management, appropriate interventions, and a high standard of safety and quality throughout their eye care journey.
Effective interprofessional communication is fundamental to achieving successful patient outcomes. The healthcare team must establish clear communication channels to facilitate the exchange of information, treatment plans, and progress updates. Regular meetings and shared electronic health records promote seamless coordination and foster a patient-centered approach to care. For instance, when addressing refractive errors or eye diseases, ophthalmologists, optometrists, and opticians collaborate closely to ensure accurate prescription, proper fitting of glasses or contact lenses, possible surgical intervention, and timely follow-up.[32][33][34]
Media
(Click Image to Enlarge)
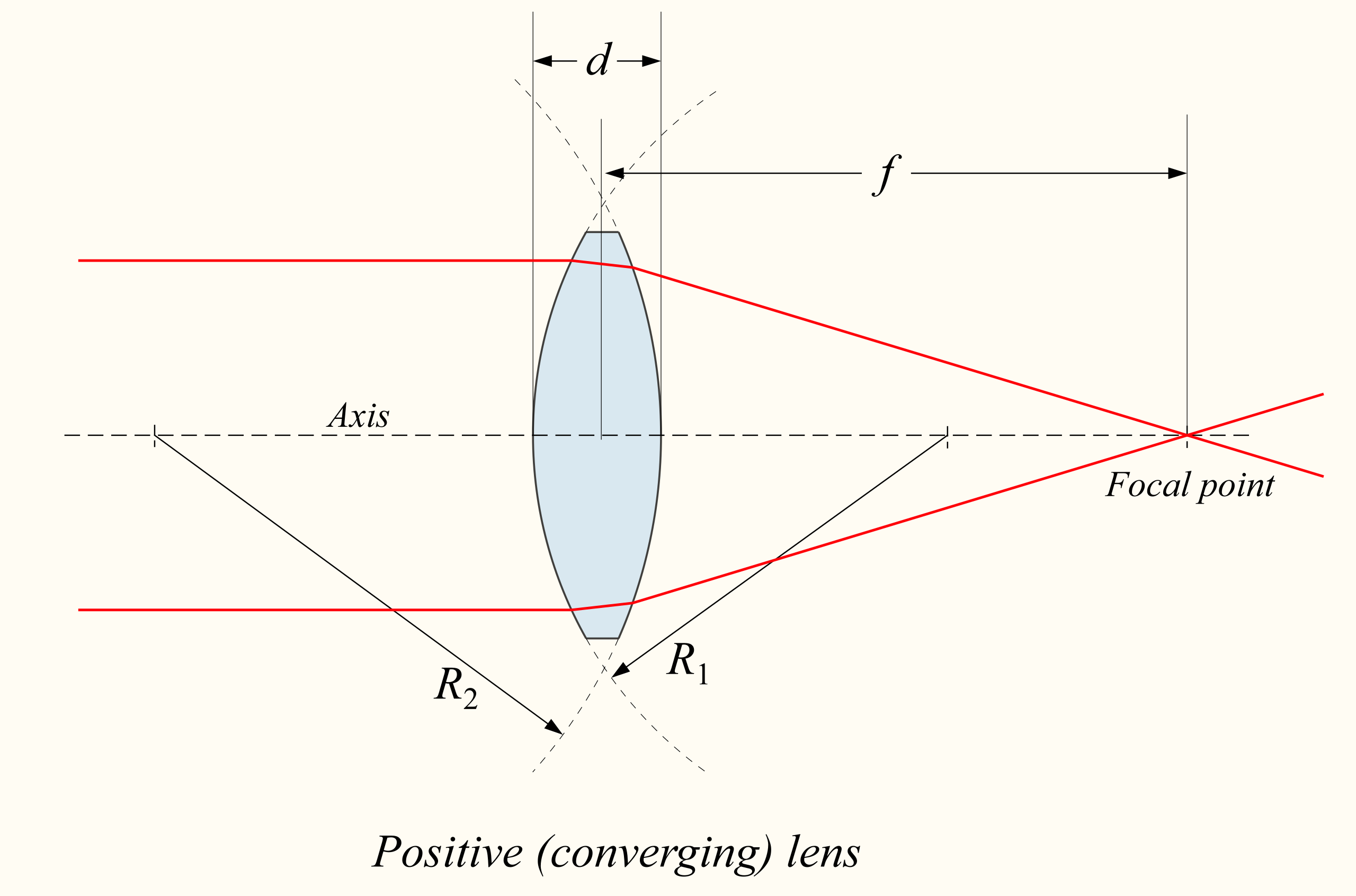
Schematic: Convex Lens. Convex, positive, or converging lenses bring parallel light rays together to converge at a specific point on the other side of the lens. The point at which these rays converge is known as the focal point, and the distance from the lens to the focal point is the focal length (f) of the lens.
DrBob, CC BY 3.0, via Wikipedia.
(Click Image to Enlarge)

Photograph: Convex Lens. A photograph of a convex or converging lens bringing parallel light rays together to converge at a specific point on the other side of the lens.
Fir0002, CC BY 3.0, via Wikipedia.
(Click Image to Enlarge)
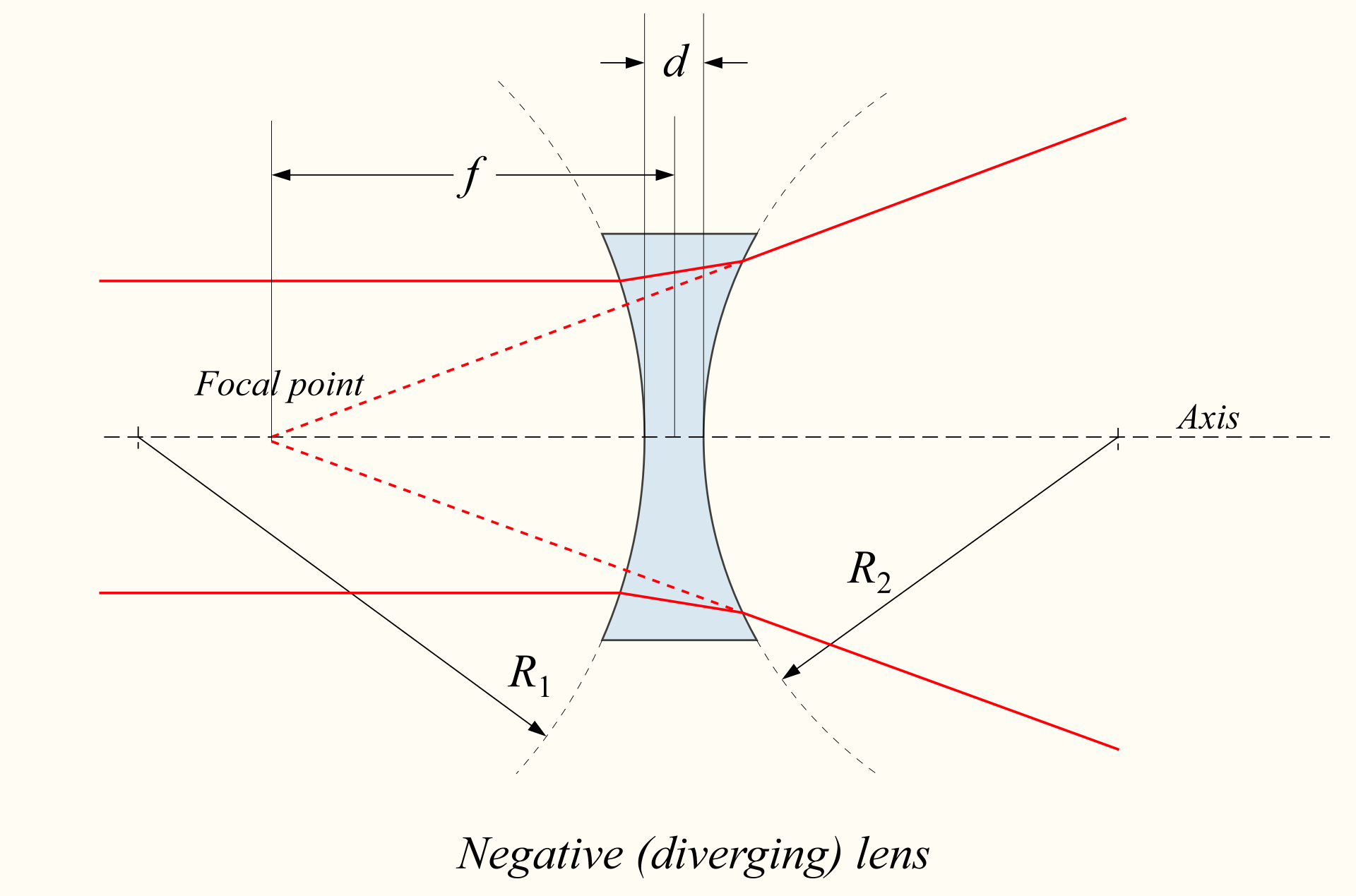
Schematic: Concave Lens. Concave lenses, also known as diverging or negative lenses, cause parallel light rays to diverge as they pass through the lens. Diverging lenses have a virtual focal point from which the divergent rays appear to originate when projected backward and creates an image behind the lens.
Wikipedia D at E, CC BY 3.0, via Wikimedia Commons.
(Click Image to Enlarge)

Photograph: Concave Lens. A photograph of a concave or diverging lens causing parallel light rays to diverge as they pass through the lens. Diverging lenses have a virtual focal point from which the divergent rays appear to originate when projected backward and create an image behind the lens.
Fir0002, CC BY 3.0, via Wikipedia.
(Click Image to Enlarge)
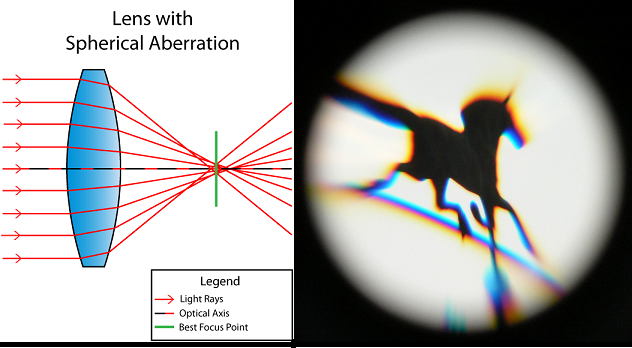
Lens With Spherical Aberration. The diagram demonstrates spherical aberration, which occurs when light rays passing through different parts of a spherical lens converge at varying focal points, resulting in blurred and distorted images. This aberration is caused by the curvature of the lens surface and the unequal bending of light rays. As a result, light rays passing through the outer region of the lens focus closer to the lens, while rays passing through the central region focus farther away.
Varenova Arina, CC BY 4.0 via Wikimedia Commons.
References
Simpson MJ. Focal length, EFL, and the eye. Applied optics. 2023 Mar 1:62(7):1853-1857. doi: 10.1364/AO.481805. Epub [PubMed PMID: 37132938]
Banks MS, Cooper EA, Piazza EA. Camera Focal Length and the Perception of Pictures. Ecological psychology : a publication of the International Society for Ecological Psychology. 2014 Jan 1:26(1-2):30-46 [PubMed PMID: 25089080]
Level 2 (mid-level) evidenceGarber N. Basic manual lensometry: a guide for measuring distance and near glasses. Journal of ophthalmic nursing & technology. 2000 Jul-Aug:19(4):184-91; quiz 192-3 [PubMed PMID: 11309995]
Enaholo ES, Musa MJ, Zeppieri M. The Spherical Equivalent. StatPearls. 2023 Jan:(): [PubMed PMID: 36943975]
Kolb H, Fernandez E, Nelson R, Carr BJ, Stell WK. The Science Behind Myopia. Webvision: The Organization of the Retina and Visual System. 1995:(): [PubMed PMID: 29266913]
Olson RJ, Waters SW. The clinical use, accuracy, and reliability of the Veri-Vu lensometer. Archives of ophthalmology (Chicago, Ill. : 1960). 1980 Nov:98(11):2060-1 [PubMed PMID: 7436845]
Jin H, Rabsilber T, Ehmer A, Borkenstein AF, Limberger IJ, Guo H, Auffarth GU. Comparison of ray-tracing method and thin-lens formula in intraocular lens power calculations. Journal of cataract and refractive surgery. 2009 Apr:35(4):650-62. doi: 10.1016/j.jcrs.2008.12.015. Epub [PubMed PMID: 19304085]
Level 2 (mid-level) evidenceTenney SR, Moshirfar M, Ronquillo Y. Concave And Convex Lenses. StatPearls. 2023 Jan:(): [PubMed PMID: 36512657]
Baird PN, Saw SM, Lanca C, Guggenheim JA, Smith Iii EL, Zhou X, Matsui KO, Wu PC, Sankaridurg P, Chia A, Rosman M, Lamoureux EL, Man R, He M. Myopia. Nature reviews. Disease primers. 2020 Dec 17:6(1):99. doi: 10.1038/s41572-020-00231-4. Epub 2020 Dec 17 [PubMed PMID: 33328468]
Mafusire C, Forbes A. Mean focal length of an aberrated lens. Journal of the Optical Society of America. A, Optics, image science, and vision. 2011 Jul 1:28(7):1403-9. doi: 10.1364/JOSAA.28.001403. Epub [PubMed PMID: 21734739]
Gurnani B, Kaur K. Astigmatism. StatPearls. 2023 Jan:(): [PubMed PMID: 35881747]
Feldkämper M, Schaeffel F. Interactions of genes and environment in myopia. Developments in ophthalmology. 2003:37():34-49 [PubMed PMID: 12876828]
Level 3 (low-level) evidenceMajumdar S, Tripathy K. Hyperopia. StatPearls. 2023 Jan:(): [PubMed PMID: 32809551]
Singh P, Tripathy K. Presbyopia. StatPearls. 2023 Jan:(): [PubMed PMID: 32809403]
Katz JA, Karpecki PM, Dorca A, Chiva-Razavi S, Floyd H, Barnes E, Wuttke M, Donnenfeld E. Presbyopia - A Review of Current Treatment Options and Emerging Therapies. Clinical ophthalmology (Auckland, N.Z.). 2021:15():2167-2178. doi: 10.2147/OPTH.S259011. Epub 2021 May 24 [PubMed PMID: 34079215]
Gupta A, Singh P. Intraocular Lens Power Calculation. StatPearls. 2023 Jan:(): [PubMed PMID: 36943961]
Chang DF. Disruptive Innovation and Refractive IOLs: How the Game Will Change With Adjustable IOLs. Asia-Pacific journal of ophthalmology (Philadelphia, Pa.). 2019 Nov-Dec:8(6):432-435. doi: 10.1097/APO.0000000000000266. Epub [PubMed PMID: 31789644]
Reiner J. [Evaluation of intraocular lenses]. Klinische Monatsblatter fur Augenheilkunde. 1990 Jul:197(1):72-5 [PubMed PMID: 2395308]
Kanclerz P, Toto F, Grzybowski A, Alio JL. Extended Depth-of-Field Intraocular Lenses: An Update. Asia-Pacific journal of ophthalmology (Philadelphia, Pa.). 2020 May-Jun:9(3):194-202. doi: 10.1097/APO.0000000000000296. Epub [PubMed PMID: 32511121]
Alio JL, Plaza-Puche AB, Férnandez-Buenaga R, Pikkel J, Maldonado M. Multifocal intraocular lenses: An overview. Survey of ophthalmology. 2017 Sep-Oct:62(5):611-634. doi: 10.1016/j.survophthal.2017.03.005. Epub 2017 Mar 31 [PubMed PMID: 28366683]
Level 3 (low-level) evidencePepose JS, Burke J, Qazi MA. Benefits and barriers of accommodating intraocular lenses. Current opinion in ophthalmology. 2017 Jan:28(1):3-8 [PubMed PMID: 27653608]
Level 3 (low-level) evidenceMoshirfar M, Bennett P, Ronquillo Y. Laser In Situ Keratomileusis (LASIK). StatPearls. 2023 Jan:(): [PubMed PMID: 32310430]
Salah-Mabed I, Moran S, Perez E, Debellemanière G, Gatinel D. Anatomical and Visual Outcomes after LASIK Performed in Myopic Eyes with the WaveLight® Refractive Suite (Alcon® Laboratories Inc., USA). Journal of ophthalmology. 2020:2020():7296412. doi: 10.1155/2020/7296412. Epub 2020 Oct 3 [PubMed PMID: 33083051]
Piao J, Whang WJ, Joo CK. Comparison of visual outcomes after femtosecond laser-assisted LASIK versus flap-off epipolis LASIK for myopia. BMC ophthalmology. 2020 Jul 29:20(1):310. doi: 10.1186/s12886-020-01579-7. Epub 2020 Jul 29 [PubMed PMID: 32727402]
Taneri S, Knepper J, Rost A, Dick HB. [Long-term outcomes of PRK, LASIK and SMILE]. Der Ophthalmologe : Zeitschrift der Deutschen Ophthalmologischen Gesellschaft. 2022 Feb:119(2):163-169. doi: 10.1007/s00347-021-01449-7. Epub 2021 Jul 9 [PubMed PMID: 34241701]
Peng W, Li H, Xu Y, Yan L, Tang Z, Tang X, Fu X. Near-focus mode for accurate operation during endoscopic submucosal tunneling procedure. Minimally invasive therapy & allied technologies : MITAT : official journal of the Society for Minimally Invasive Therapy. 2022 Jan:31(1):99-106. doi: 10.1080/13645706.2020.1768408. Epub 2020 May 23 [PubMed PMID: 32449398]
Paradis TJ, Dixon J, Tieu BH. The role of bronchoscopy in the diagnosis of airway disease. Journal of thoracic disease. 2016 Dec:8(12):3826-3837. doi: 10.21037/jtd.2016.12.68. Epub [PubMed PMID: 28149583]
Sluder G, Nordberg JJ. Microscope basics. Methods in cell biology. 2013:114():1-10. doi: 10.1016/B978-0-12-407761-4.00001-4. Epub [PubMed PMID: 23931500]
Boyce SJ, Samei E. Imaging properties of digital magnification radiography. Medical physics. 2006 Apr:33(4):984-96 [PubMed PMID: 16696475]
Shimakawa Y, Nishiki M, Yanagita S, Nishikawa N, Sakai T, Ito H, Ochi S, Yanagawa N. Evaluation of x-ray effective focal spot size dependency on x-ray exposure settings using edge response analysis. Radiological physics and technology. 2023 Mar:16(1):39-47. doi: 10.1007/s12194-022-00688-w. Epub 2022 Dec 14 [PubMed PMID: 36515865]
Qin Y, Hua H. Optical design and system engineering of a multiresolution foveated laparoscope. Applied optics. 2016 Apr 10:55(11):3058-68. doi: 10.1364/AO.55.003058. Epub [PubMed PMID: 27139875]
Level 2 (mid-level) evidenceBudning A, El-Defrawy S. Interprofessional collaboration in eye health care. Canadian journal of ophthalmology. Journal canadien d'ophtalmologie. 2016 Jun:51(3):130-2. doi: 10.1016/j.jcjo.2016.04.007. Epub [PubMed PMID: 27316255]
Rahmani M, Ortiz-Toquero S, Martin R. Referral pattern and co-management of keratoconus patients in primary eye care: A survey of three European countries. Contact lens & anterior eye : the journal of the British Contact Lens Association. 2022 Jun:45(3):101518. doi: 10.1016/j.clae.2021.101518. Epub 2021 Nov 10 [PubMed PMID: 34772626]
Level 3 (low-level) evidenceChan SCY, Shah PR, Tan K, Ford B, Webber A, Keay L. Integration of hospital and community care for paediatric ophthalmology: A mixed-methods study. Ophthalmic & physiological optics : the journal of the British College of Ophthalmic Opticians (Optometrists). 2023 Sep:43(5):997-1006. doi: 10.1111/opo.13160. Epub 2023 May 7 [PubMed PMID: 37150970]
