Definition/Introduction
Healthcare professionals, when determining the impact of patient interventions in clinical studies or research endeavors that provide evidence for clinical practice, must distinguish well-designed studies with valid results from studies with research design or statistical flaws. This article will help providers determine the likelihood of type I or type II errors and judge adequacy of statistical power. Then one can decide whether or not the evidence provided should be implemented in practice or used to guide future studies.
Issues of Concern
Having an understanding of the concepts discussed in this article will allow healthcare providers to accurately and thoroughly assess the results and validity of medical research. Without an understanding of type I and II errors and power analysis, clinicians could make poor clinical decisions without evidence to support them.
Type I and Type II Errors
Type I and Type II errors can lead to confusion as providers assess medical literature. A vignette that illustrates the errors is the Boy Who Cried Wolf. First, the citizens commit a type I error by believing there is a wolf when there is not. Second, the citizens commit a type II error by believing there is no wolf when there is one.
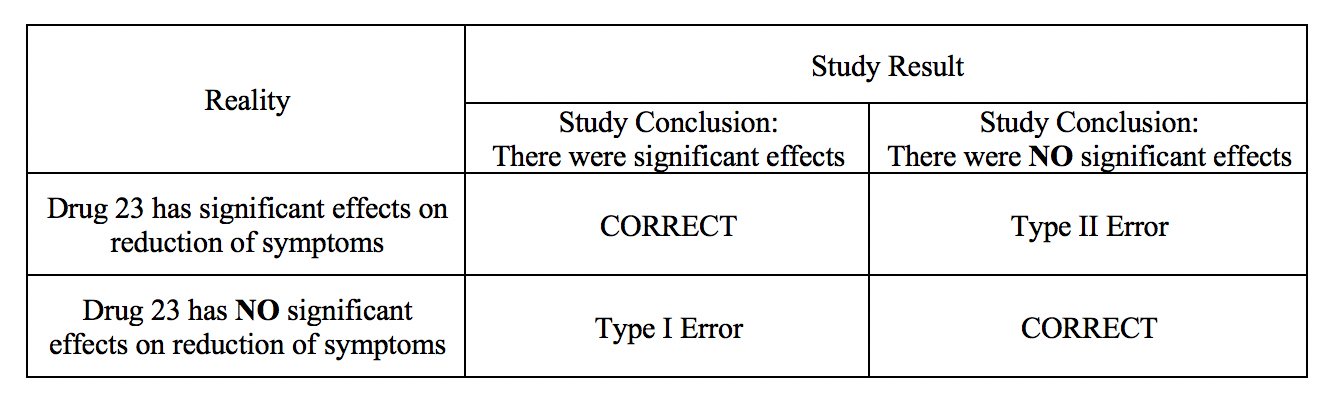
A type I error occurs when in research when we reject the null hypothesis and erroneously state that the study found significant differences when there indeed was no difference. In other words, it is equivalent to saying that the groups or variables differ when, in fact, they do not or having false positives.[1] An example of a research hypothesis is below:
Drug 23 will significantly reduce symptoms associated with Disease A compared to Drug 22.
For our example, if we were to state that Drug 23 significantly reduced symptoms of Disease A compared to Drug 22 when it did not, this would be a type I error. Committing a type I error can be very grave in specific scenarios. For example, if we did, move ahead with Drug 23 based on our research findings even though there was actually was no difference between groups, and the drug costs significantly more money for patients or has more side effects, then we would raise healthcare costs, cause iatrogenic harm, and not improve clinical outcomes. If a p-value is used to examine type I error, the lower the p-value, the lower the likelihood of the type I error to occur.
A type II error occurs when we declare no differences or associations between study groups when, in fact, there was.[2] As with type I errors, type II errors in certain cause problems. Picture an example with a new, less invasive surgical technique that was developed and tested in comparison to the more invasive standard care. Researchers would seek to show no differences between patients receiving the two treatment methods in health outcomes (noninferiority study). If, however, the less invasive procedure resulted in less favorable health outcomes, it would be a severe error. Table 1 provides a depiction of type I and type II errors.
(See Type I and Type II Errors and Statistical Power Table 1)
Power
A concept closely aligned to type II error is statistical power. Statistical power is a crucial part of the research process that is most valuable in the design and planning phases of studies, though it requires assessment when interpreting results. Power is the ability to correctly reject a null hypothesis that is indeed false.[3] Unfortunately, many studies lack sufficient power and should be presented as having inconclusive findings.[4] Power is the probability of a study to make correct decisions or detect an effect when one exists.[3][5]
The power of a statistical test is dependent on: the level of significance set by the researcher, the sample size, and the effect size or the extent to which the groups differ based on treatment.[3] Statistical power is critical for healthcare providers to decide how many patients to enroll in clinical studies.[4] Power is strongly associated with sample size; when the sample size is large, power will generally not be an issue.[6] Thus, when conducting a study with a low sample size, and ultimately low power, researchers should be aware of the likelihood of a type II error. The greater the N within a study, the more likely it is that a researcher will reject the null hypothesis. The concern with this approach is that a very large sample could show a statistically significant finding due to the ability to detect small differences in the dataset; thus, utilization of p values alone based on a large sample can be troublesome.
It is essential to recognize that power can be deemed adequate with a smaller sample if the effect size is large.[6] What is an acceptable level of power? Many researchers agree upon a power of 80% or higher as credible enough for determining the actual effects of research studies.[3] Ultimately, studies with lower power will find fewer true effects than studies with higher power; thus, clinicians should be aware of the likelihood of a power issue resulting in a type II error.[7] Unfortunately, many researchers, and providers who assess medical literature, do not scrutinize power analyses. Studies with low power may inhibit future work as they lack the ability to detect actual effects with variables; this could lead to potential impacts remaining undiscovered or noted as not effective when they may be.[7]
Medical researchers should invest time in conducting power analyses to sufficiently distinguish a difference or association.[3] Luckily, there are many tables of power values as well as statistical software packages that can help to determine study power and guide researchers in study design and analysis. If choosing to utilize statistical software to calculate power, the following are necessary for entry: the predetermined alpha level, proposed sample size, and effect size the investigator(s) is aiming to detect.[2] By utilizing power calculations on the front end, researchers can determine adequate sample size to compute effect, and determine based on statistical findings; sufficient power was actually observed.[2]
Clinical Significance
By limiting type I and type II errors, healthcare providers can ensure that decisions based on research outputs are safe for patients.[8] Additionally, while power analysis can be time-consuming, making inferences on low powered studies can be inaccurate and irresponsible. Through the utilization of adequately designed studies through balancing the likelihood of type I and type II errors and understanding power, providers and researchers can determine which studies are clinically significant and should, therefore, implemented into practice.
Nursing, Allied Health, and Interprofessional Team Interventions
All physicians, nurses, pharmacists, and other healthcare professionals should strive to understand the concepts of Type I and II errors and power. These individuals should maintain the ability to review and incorporate new literature for evidence-based and safe care. They will also more effectively work in teams with other professionals.