Definition/Introduction
Utilizing pharmacy calculations to administer therapeutics to patients correctly is vital to patient treatment. Health care professionals must dispense drugs in the accurate concentrations, calculate correct doses, and compound and prepare medications accurately to ensure that each particular drug is being administered correctly.
Dose refers to the amount of medication taken at a specific time, whereas the dosage of the drug refers to the administration of a frequency, amount, and the number of doses taken over a particular period of time.
The following definitions can aid in preparing and administering pharmacological drugs.
Concentration is the amount of active ingredient per total weight of a substance.
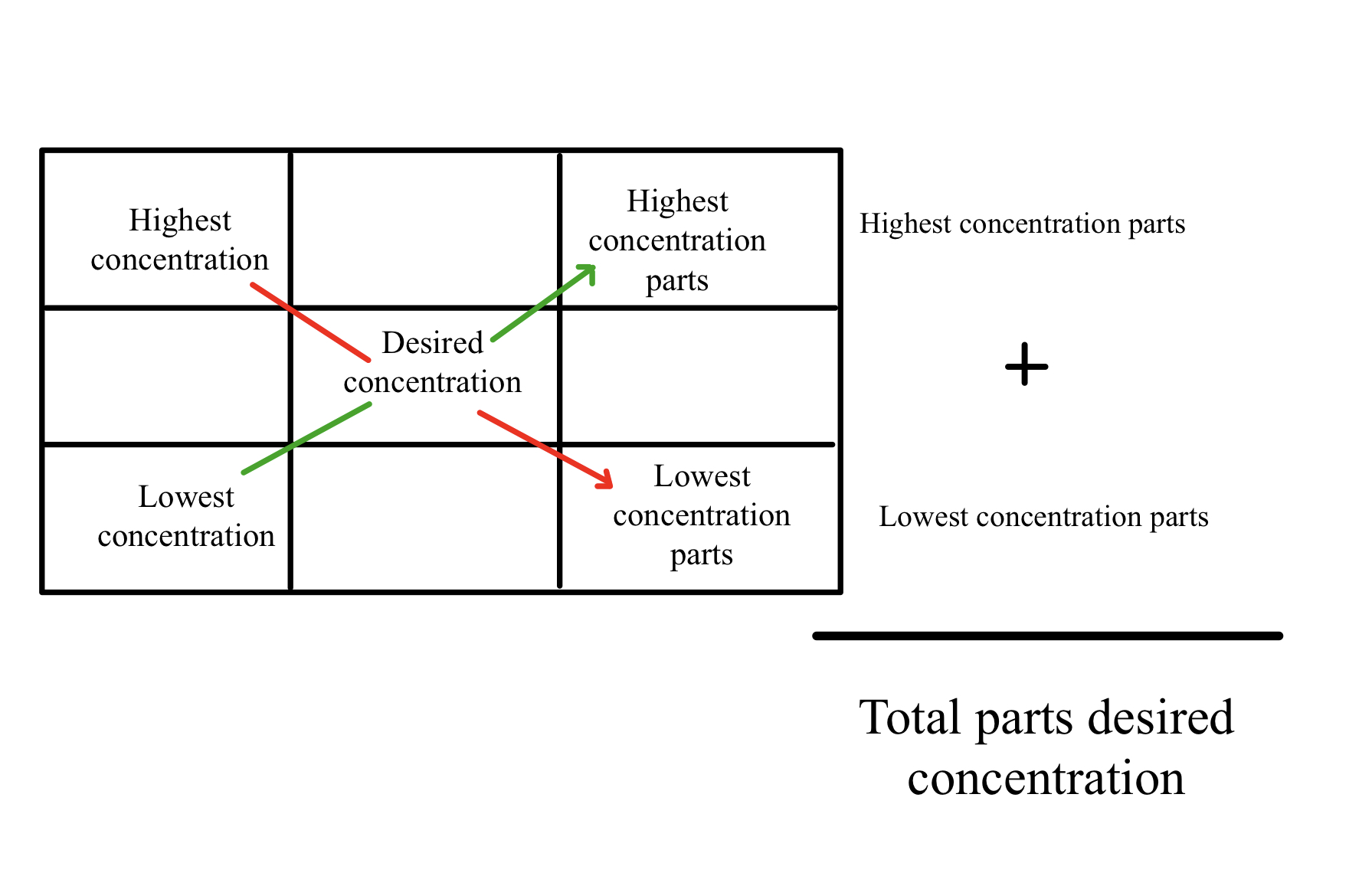
Alligation involves mixing solutions or solids of varying strengths to obtain another strength of the active ingredient in both.[1]
Specific gravity refers to the ratio of the weight of a substance to the weight of an equal volume of water at the same time.
Specific gravity = number of grams of a substance/number of milliliters of a substance.
If the specific gravity is known, the volume or weight of the desired quantity can be determined.
The following pharmacy calculations are used to determine the dose and dispense drugs in the correct concentrations [2]:
Tablet Dosage
Desired Dose/Stock Strength = Number of Tablets
Mixtures and Solutions
[Desired Dose/Stock Stregth] x Stock Volume = Amount of Solution to be given
IV Rate
mL per hour and minute
Total IV Volume/Time (hour or minute) = mL per hour or minute
Drops per minute
[Total IV volume/Time (minute)] X Drop Factor = Drops per minute
Remaining time of infusion
[Volume remaining (in mL)/Drop per minute] x Drop Factor = Minutes remaining [3]
Dilutions
The relationship between concentration and volume is inversely proportional. (See Figure 1 for a schematic of the inverse relationship between percent of concentration or ratio strength (decreases), and the total quantity of product (increases)).
Thus, if a solution requires a dilution, the active drug in the solution will remain constant, but the volume will increase. [4]
Isotonicity:
It is important to note that when two solutions have equal osmotic pressure and salt concentration, they are said to be isotonic. Normal saline has a concentration of 0.90% w/v of NaCl in sterile water and therefore is an isotonic crystalloid.[5]
Percent Strength[6]:
Percent strength represents the number of grams contained in 100 mL of product and is very useful in pharmacy calculations.
The following units express percent based on the nature of the ingredient:
Percent Weight in Volume (w/v): Is the number of grams in 100 mL of solution and is expressed as %w/v. Powdered substances suspended in a liquid vehicle would be calculated as w/v.
Percent Volume in Volume (v/v): Is the number of milliliters in 100 mL of solution and is expressed as %v/v. A liquid component in a liquid preparation would be calculated on a v/v basis.
Percent weight in weight (w/w): Is the number of grams in 100 grams of solution and is expressed as %w/w. Powdered substances mixed with a solid or semisolid (ointments) would be calculated as w/w.
Issues of Concern
Accurate pharmacy calculations prevent medical errors; underdosing a patient may lead to inadequate treatment, and overdosing a patient may lead to drug toxicity.
Additionally, pharmacy calculations require the knowledge of commonly used units; certain medications are dispensed in metric system units such as mg or mL, whereas others may be dispensed in other measurement systems. Vitamin D, for instance, is administered in International Units.[7]
Drugs may be administered through various routes of administration, oral, IV, IM, parenteral, etc.; these factors must be accounted for when computing calculations and consistency when converting units across different measurement systems is important in maintaining accuracy in pharmacy calculations. This issue also impacts patient care as patients may use the household and avoirdupois systems when using their medications (teaspoons and tablespoons), although the medication was dispensed in mL. It is important to know units within each system (such as 1 pound = 16 ounces). quantity, conversions are required between the US Customary System and the metric unit system.[8] Some commonly used conversions are:
- 2.2 pounds = 1 kg
- 1 solid ounce = 30 g
- 1 tablespoon = 15 mL
- 1 teaspoon = 5 mL
- 1 liquid oz = 30 mL
Conversion calculations may also occur in other measurements, such as time and temperature.
The following equations can be used to convert degrees Fahrenheit to Celcius and vice versa [7]:
Degrees C to degrees F: Divide by 5, then multiply by 9, then add 32
Degrees F to degrees C: Subtract 32, then multiply by 5, then divide by 9
Roman numerals are often used on prescriptions as they are challenging to alter, whereas decimals are also used elsewhere in pharmacy practices. Measurements requiring decimals are usually converted into fractions; thus, familiarity with converting measurements between various systems and a foundation in basic arithmetics in terms of fractions, ratios, proportions, and percent is necessary to perform pharmacy calculations.
The aliquot method consists of measuring out a small amount of drug, by diluting a larger amount. Aliquoting plays an essential role as a technique to separate a larger sample into smaller parts; it is also equally as important in temperature sensitivity of drugs.[9]
Lastly, stock solutions exist to dispense medications to patients. However, certain patients require different concentrations of drugs, and the Alliqation method exists to calculate and dispense correction concentrations of active ingredients for patients. (See Figure 2 for a schematic of the Alligation method).[10]
Clinical Significance
It may also be important to account for patients' weight when calculating the correct dose for certain drugs. The body surface area represents the patient's height and weight. In certain patient populations, specific drugs may be dosed based on BSA depending on drug properties. The average adult has a BSA of 1.73 m^2. The equation for BSA may be calculated as follows:
- BSA (m^2) = [Height (inches) x Weight (lbs)/3131]^1/2.[11]
The following are the calculations for ideal body weight for males and females, respectively[12]:
- Male: IBW = 51.65 kg + 1.85 kg/inch of height greater than 5 feet
- Female IBW = 48.67 kg + 1.65 kg/inch of height greater than 5 feet
The pediatric population often utilizes Young's Rule (pediatric dose based on age) or Clark's Rule (pediatrics dose based on weight) to determine the dose administered.[13]
It is also important to note that some drugs may be dispensed in their own respective units; for instance, the drug digitalis is dosed as follows:
The number of vials of digitalis required = Total digitalis body load X 0.8/0.5 mg of digitalis bound.[14]
In regards to toxicity, understanding properties of certain drugs is important in order to eliminate them effectively. For acidic drugs: pH = pKa + log [A-]/[AH] and for basic drugs: pH = pKa + log[B]/[BH+].[15]
Nursing, Allied Health, and Interprofessional Team Interventions
In addition to pharmacy calculations, other factors in pharmacology must also be a consideration. For instance, bioavailability is the amount of drug from the administered dose that reaches the systemic circulation and should be taken into account. Different routes of administrations can impact drug bioavailability.
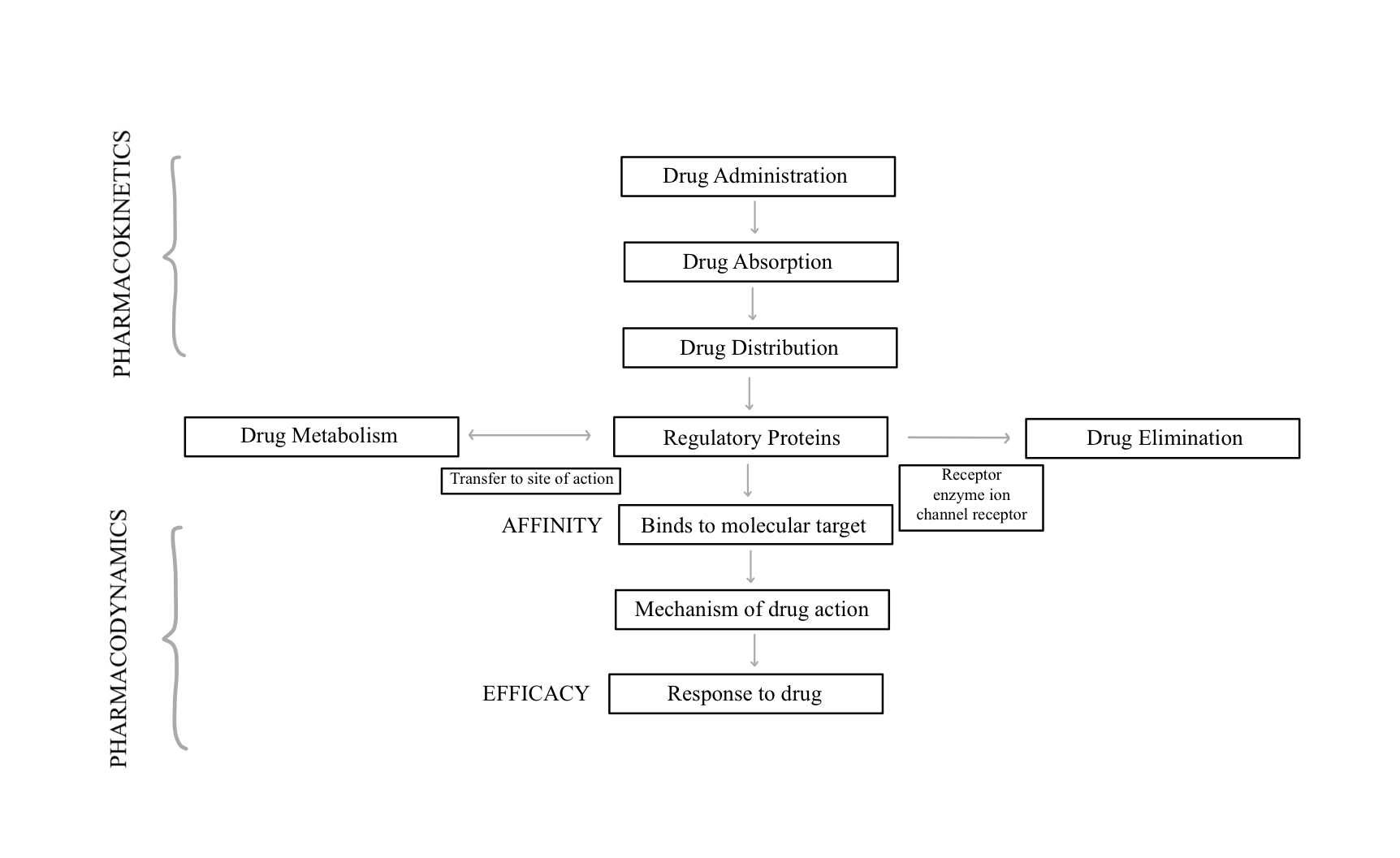
It is essential to understand the relationship between pharmacokinetics and pharmacodynamics as these factors influence the drug effect and metabolism. (See Figure 3 for a schematic of the relationship between pharmacokinetics and pharmacodynamics.)
Pharmacodynamics is the study of drug effects and their metabolism of action.[16] Understanding potency of a drug (the amount of medication required to a given intensity of effect) and efficacy of the drug (maximum response achievable), and whether the drug has agonist or antagonist properties. Pharmacokinetics is the study of the time required for the drug to be absorbed, distributed, metabolized, and eliminated (ADME).[16]
Nursing, Allied Health, and Interprofessional Team Monitoring
Accurate pharmacy calculations are not only necessary for dispensing, dosing, and adequately medicating patients but also a vital component of pharmacological therapy, effect, and, ultimately, patient care. The interprofessional health care team must work together to determine and administer adequate pharmacological treatment to patients. Specifically, differing patient populations may have varying needs. Liver and kidney dysfunction can alter the metabolism of a drug, as can age.[17] Beers criteria are often used to determine which drugs to avoid in the elderly patient.[18] Thus, the accuracy of pharmacy calculations remains an important component of pharmacologic therapy and patient care.